Cats2D Multiphysics > Research Topics > Kármán vortex street
A stroll down the Kármán vortex street
Unpublished results Copyright © 2019 Andrew Yeckel, all rights reserved
Posted on October 3, 2019
Art works generated by this flow can be viewed in my new Vortex Street collection.
1. Introduction
Flow past a circular cylinder makes an excellent test problem for validating Cats2D, and also a great subject for visualization. It is one of the best studied problems of all time in fluid dynamics, making it possible to compare the code closely against numerous features that have been carefully documented for this fascinating flow. I report here what I have learned from simulating this problem for Reynolds number up to 300, approximately the upper limit for laminar flow.
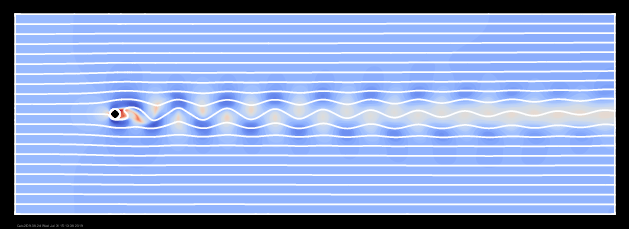
A sequence of flow visualizations by Taneda is featured in Van Dyke's An Album of Fluid Motion (cover image, images 94 to 96). The cover image, below left, is compared to a Cats2D simulation, below right. The Reynolds number is 140. The agreement is good, but not perfect. I dig into these differences in later sections of this article.

A similar sequence by Homann is shown in Batchelor's An Introduction to Fluid Dynamics (plate 2), and another by Tritton can be found in his book Physical Fluid Dynamics, 2nd edition (figure 3.5), the third chapter of which is devoted to flow past a circular cylinder. A deeper look can be found in this contribution to Annual Review of Fluid Mechanics by C.H.K. Williamson. However, none of these sources have much in the way of simulations, all of them predating 1996.
All these studies have found that flow behind the cylinder is quite sensitive to Reynolds number. According to Tritton, the following transitions are observed in the laminar regime:
—At Reynolds number around 4, flow separates at the rear of the cylinder forming two small vortexes.
—At Reynolds number around 40, flow behind the cylinder begins to oscillate gently.
—At Reynolds number around 100, periodic shedding of vortexes from the cylinder is observed.
—At Reynolds number between 150 and 200, flow begins to oscillate with unstable period and amplitude.
—At Reynolds number above 300, turbulence is observed.
There are other significant changes in the appearance of the wake as the Reynolds number is varied in this range, such as the formation of distinctive cusps and curls in the streaklines for which this flow is famous. There is some variability among the experiments in the precise value of Reynolds number at which these transitions are observed, but there is agreement that the transitions are rather sudden and quite sensitive to the conditions of the experiment.
My initial aims were to reproduce a few experimental photographs, and to determine the values of Reynolds numbers at which the transitions described above occur. I intended this primarily as a validation of Cats2D, but I have learned this flow is more interesting than I had supposed, so I have used the unique tools of Cats2D to analyze and visualize how the flow evolves during these transitions.
My observations mostly confirm what is already known about this flow, but in some ways my findings contradict or supplement it. After I present my validation studies below, I use my results to challenge the notion of vortex shedding as it has been commonly used to conceptualize this flow. In particular I show that the third transition described above does not exist; vortex shedding is concomitant with the second transition, but is difficult to perceive visually.
2. Conditions of the simulations
Simulations were computed mostly on two domains, both of which extend 50 cylinder diameters downstream of the cylinder. The narrower domain extends 10 cylinder diameters to each side and upstream of the cylinder. The wider domain extends 50 cylinder diameters to each side and 20 cylinder diameters upstream of it.
Except as noted, boundary conditions are uniform flow at the inlet, zero flow through the sides, free slip along the sides, and zero streamwise velocity gradient at the outlet. A few tests were performed with periodic conditions imposed at the sides, with no other restrictions on the flow there. Other tests were performed with parabolic flow at the inlet and no-slip boundary conditions at the sides.
These boundary conditions represent a physical situation comparable to flow in a wide channel past a stationary cylinder. Some of the experiments discussed below were conducted this way, either in a wind tunnel or a channel of flowing liquid. A common alternative is to drag the cylinder through a large stationary tank of liquid with a camera attached to the moving cylinder. The same model equations apply here when viewed in the reference frame of the moving cylinder. This type of experiment is better able to represent an infinite free stream because the wall and free stream are both stationary in the laboratory frame. In the wind tunnel or channel flow experiments, the free stream is forced to zero at the wall, which perturbs flow near the cylinder.
Over 550,000 degrees of freedom were used to remove any doubts about discretization accuracy. The non-dissipative trapezoid rule was used with at least 100 and up to 400 time steps per period to ensure small time integration error. Eigenvalues were computed using Sorenson's ARPACK. All other details of the implementation are found in the Cats2D user manual.
Symmetric steady state solutions exist at all Reynolds numbers studied here. The grid is structured and symmetric, enabling Cats2D to compute a symmetric steady state very precisely. The instability is very slow to develop from "noise" in the numerics, so I used a few strategies to incite it more quickly. In some cases I used the solution at Re = 0 as an initial condition, changing Reynolds number to the target value before starting the time integration. In other cases I computed the steady state at the target Reynolds number with the inlet velocity perturbed in the lateral direction (1,0.0001), restoring it to an unperturbed (1,0) before starting the time integration. Both methods worked well.
In the following sections I compare simulations to empirical results for shedding frequency and drag force. Then I compare Cats2D visualizations to photographs published by several different researchers, including Taneda, Homann, Tritton, and others. After that I use eigenanalysis and time integration experiments to determine the critical Reynolds numbers for key flow transitions. Lastly I examine the issue of how a vortex is defined, which is a matter of reference frame, but also visual perception.
3. Visualizing the flow
Many photographs have been published for this system. Most of the visualizations shown below are streamlines or streaklines of some sort, depending on the particular experimental photograph I am attempting to reproduce by simulation. Streaklines are visualized by continuously injecting an agent (dye, smoke) upstream of the cylinder or from its surface. Instantaneous streamlines are visualized by dispersing small reflective particles (aluminum dust, glass beads) throughout the liquid and using a long exposure time. The two representations look very different for unsteady flow.
Simulations of flow past a cylinder are rarely visualized well, despite the flow being so photogenic in nature. I show here four different animated visualizations of the flow at Re = 140. Instantaneous streamlines oscillate spatially and temporally, but otherwise give little indication of the rich structure displayed by the streaklines so often photographed in experiments:

Particle paths also fail to convey much about the nature of this flow except that it is oscillatory:

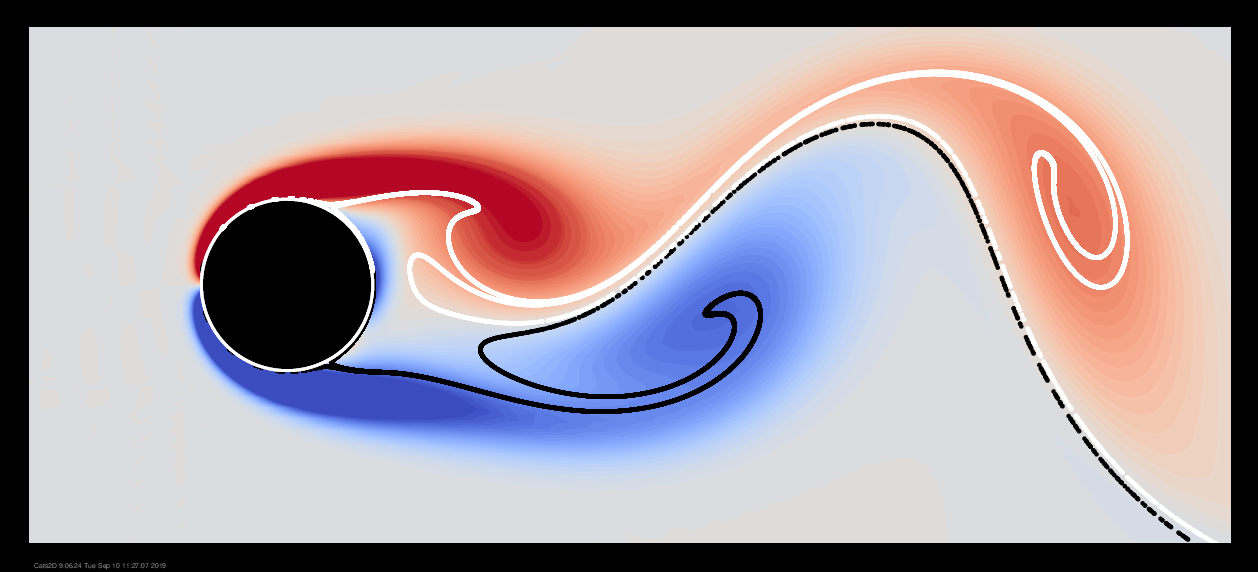
Particle streaklines are difficult to compute in a time-dependent flow, so simulations are often visualized by vorticity without any explanation as to why it should be compared to a streakline visualization, relying instead on the obvious similarity between the two to carry the message:

We can see in the animation that streaklines do travel along paths of large vorticity, positive or negative, but vorticity plots alone are insufficient to make accurate comparisons to photographs of experiments. Any serious attempt to visualize this flow should use streaklines instead.
It is particularly rewarding to compute critical point streamlines, because it shows exactly how the vortexes form and detach from the cylinder:

A vortex swells, then detaches from the rear of the cylinder. After it detaches, the vortex is delineated by a saddle streamline that snakes around the cylinder, rather than by a separation streamline attached to the cylinder. The vortex quickly diminishes in size and vanishes before the next vortex detaches from the cylinder. This contradicts the prevailing view, based on conjecture by Perry et al in 1982, that the vortex persists and moves downstream after it detaches, coexisting with other vortexes that have detached before and after it.
4. Quantitative validations
The Strouhal number and drag coefficient have been measured in many different experiments for this system. By now a narrow range of values has been established for these quantities. A good simulation can and should match the established values to within a few percent.
At steady state, the flow divides evenly around the two sides of the cylinder. When the instability is active, it no longer does so. Velocity alternates between faster and slower around each side of the cylinder, causing the stream function to oscillate at the front and rear of it. I set up Cats2D to monitor this oscillation on the trailing axis of the cylinder to measure the vortex shedding frequency, discussed in the next section.
Strouhal number
The Strouhal number, fD/U, is the frequency of flow oscillation scaled by the ratio of cylinder diameter D to free stream velocity U. This number is approximately 0.2 in the laminar flow regime. A more precise empirical relationship has been published by Fey, König, and Eckelmann, St = 0.2684 - 1.0356/sqrt(Re), for the range Re = 47 to 250. This relationship is compared to simulations computed by Cats2D on the narrower domain in the plots shown below. Two different boundary conditions are considered at the sides of the domain. The sides are treated as either periodic, or with slip but impermeable to flow (labeled "confined" in the plots). Neither treatment perfectly represents the experimental situation, but the solution is insensitive to the choice.
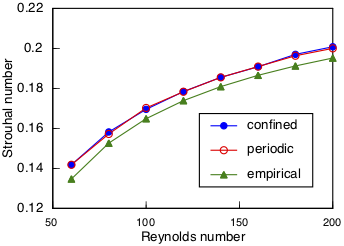
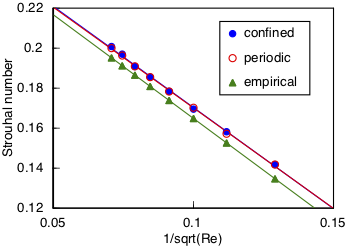
The simulation perfectly follows the square root dependence on Reynolds number. The deviation between simulation and the empirical relationship is not large, but it is systematic. At Re =140 I have solved the problem on domains with channel widths of 20, 40, and 100 cylinder diameters and plotted all the results, shown below. The curve is a quadratic fit, a Richardson extrapolation to infinite channel width, which is close to the empirical value, shown by the symbol on the y-axis.
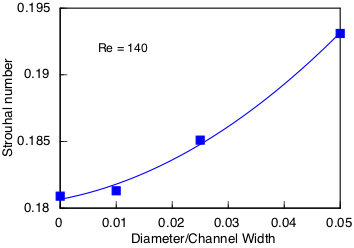
The agreement with the empirical formula is quite good if the domain is large enough. I have run simulations using a parabolic velocity profile instead of plug flow at the inlet and found it to have very little effect. I have also run simulations in which the channel width expands downstream of the cylinder, forcing the entire flow to decelerate behind it, and this too had very little effect. What matters most are the Reynolds number and the shape of the cylinder. Channel width plays a minor role by altering acceleration of the flow around the cylinder, but this effect is small unless the channel is narrow. So I don't think the excellent agreement of Strouhal number is happenstance.
Drag coefficient
The drag coefficient is a dimensionless measure of force exerted on the cylinder by the flow:
![]()
The second form is shown because Cats2D reports the quantity in brackets, which is a viscous scaling of the surface force. The results shown here are very close in value to those reported by Sheard, Hourigan, and Thompson (figure 4) in 2005.
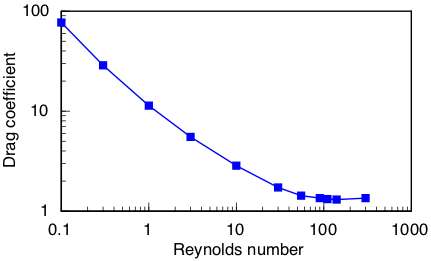
I'm satisfied with these quantitative comparisons, so let's look at some visualizations of the flow, starting at low Reynolds number.
5. Qualitative validations
Although I describe the following comparisons as qualitative, these flows have a complex structure that is very sensitive to Reynolds number. These comparisons are more demanding than the quantitative measures studied in the previous section.
Steady flow, Re < 50
Flow over a cylinder is steady and stable for Reynolds number less than around 40. The first interesting thing to happen is flow separation at the rear of the cylinder, forming two small vortexes. The vortexes are shown here at Re = 6.5, computed on the wide domain.
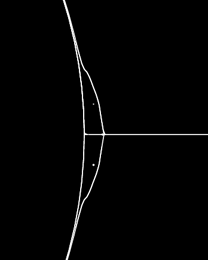
In an experiment these vortexes are hard to see when they are small, making it difficult to determine the critical Reynolds number for separation. Tritton says it occurs when Reynolds number is greater than about 4. Van Dyke writes: "Extrapolation of such experiments to unbounded flow suggests separation at Re = 4 or 5, whereas most numerical computations give Re = 5 to 7." My simulations locate separation at 6.0 < Re < 6.5 on both the narrow and wide domains. I'm sure the simulations are right, insofar that perfect conditions are met by the experiments. However, many non-idealities might contribute to early separation in the experiments, including three dimensional effects.
The vortexes elongate as Reynolds number increases. Results at Re = 13, 26, and 41 are shown below. These correspond to figures 41, 42, and 46 in Van Dyke's album, which are photographs taken by Taneda. Agreement between experiment and theory is excellent.



For Reynolds number greater than approximately 40, an unstable wake forms, yet steady state solutions can be computed to much higher values of Re. These solutions cannot be observed experimentally, but computationally there are a few points of interest about them that I discuss in the appendix below.
Periodic oscillations, 40 < Re < 200
In the streakline plots shown in the following sections, I have colored particles white or black to show whether they originate on the upper or lower surface of the cylinder.
Comparison to Homann's experiment
Below is a Cats2D simulation compared to Homann's visualization of flow over a cylinder at Re = 73, from plate 2 of Batchelor. I do not have a reference length for the photograph, and I do not know the oscillation frequency in the experiment. For this comparison I've assumed the simulation and experiment have the same frequency, which I think is justified because the simulation matches the best empirical correlation available for this flow. This allows me to size the images such that the peaks and valleys of the vortex street align as well as possible vertically.

If my assumption of equal shedding frequencies is good, it should appear that the cylinder is the same size in both of these images. The cylinder looks larger in the Cats2D simulation than in Homann's photograph, but I think this is partly an illusion. In the simulation only the black area constitutes cylinder; the thick white line around it represents a crowd of particles. I've enlarged this detail and placed identical white circles on the cylinder in each image. I've made the circle barely smaller than the cylinder diameter such that a thin halo remains in both images.

The size match appears reasonable to me, but the cylinder in the simulation does seem slightly larger. If I rescale the photograph to obtain what I think is the best matching of cylinder size, it somewhat degrades the vertical alignment of peaks and valleys, so I've made a compromise between these objectives.
Note that I might have approached this issue more directly by simply measuring the cylinder diameter in the photograph to obtain a reference length for scaling the images. But having only a low resolution image of the photograph, plus my uncertainty discerning the true cross section of the cylinder, I judged it infeasible to estimate the diameter in a convincing manner. These images show that I am in the right ballpark. If the error in scaling was worse than 10% or so, I think it would be apparent here.
I think the comparison is pretty good. Some differences between experiment and simulation can be explained by molecular diffusion, which is not represented in the simulation. But the vortex street is 15% wider in the simulation and this bears further examination. Perhaps less significant yet still noticeable is the relative position of the cusp that forms downstream of the local extrema in the particle lines. These particles lines look like a series of breaking waves to me, and in that descriptive framework, the waves appear to have broken somewhat further in the simulation than in the experiment. In the next section I show how these features can be matched more closely between experiment and simulation.
A second look at Homann's experiment
I show now that an excellent match can be found by reducing the Reynolds number in the simulation to 58, which is 20% smaller than Homann's reported value of 73:
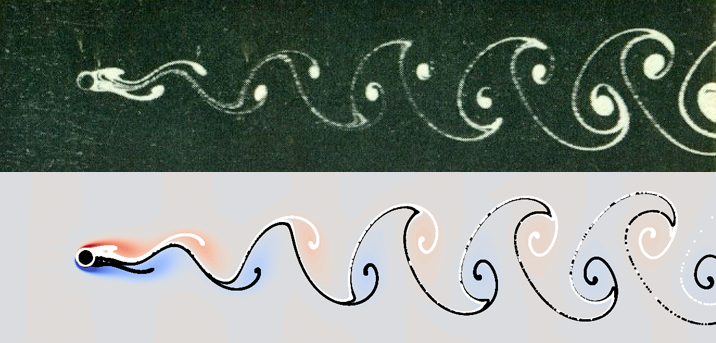
The positions of the cusps, and the extent to which the streaklines curl at the vortex centers, match the experiment much better than before. The width of the vortex street (distance between peaks and valleys) also agrees better, deviating by about 9% between experiment and simulation compared to 15% before. The matching of cylinder size also looks better than before:

I really like this comparison. Carrying on then, I compare Homann's result at Re = 65 to a Cats2D simulation at Re = 52, which is 20% smaller than Homann's value.

The effect of diffusion in the experiment is obvious, causing the sharp cusps to soften and retreat. Otherwise this is a fine match between experiment and simulation. I find another close match when I compare Homann's result at Re = 55 to a Cats2D simulation at Re = 40, which is 28% smaller than Homann's value.

Homann's results are not consistent with later experiments by Taneda, Tritton, and others, which agree that oscillations are observed at Reynolds numbers well below 50, in agreement with my simulations, rather than near 55 where Homann locates it. In the next section I show that Cats2D results agree very closely with Tritton's experiment when using the same values of Reynolds number reported by Tritton. This bolsters the conclusion that Homann's reported values have a systemic error.
Comparison to Tritton's experiment
The cylinder is only partially visible in Tritton's photographs (figure 3.5 in his book), so we can only determine the scale by assuming equal Strouhal numbers. This limits us to comparing the form of the streaklines at various Reynolds numbers rather than quantifying the amplitude or frequency, but we know that the cusps and curls of the streaklines are very sensitive to Reynolds number. Streaklines computed by Cats2D at Re = 47, 55, and 67, shown below, agree remarkably well with Tritton's experiments at the same values of Reynolds number.



Tritton also reports that the wake first begins to oscillate at Reynolds number near 40. Further down this page in another section I show that the onset of the instability occurs at 39.0 in the wide domain and 46.0 in the narrow domain.
Figure 3.8 in Tritton's book shows motion immediately behind the cylinder at Re = 110 revealed by dye released from its surface. My simulation looks similar to the photograph, except that my streaklines have curled slightly more (note that his photograph is taken below and to the right of the cylinder, distorting the shape of the streaklines in the vertical plane of the experiment):
These are pleasing comparisons. I can make them slightly better by varying channel width and Reynolds number, but they already fall well within the variability of the experiments themselves.
Comparison to Taneda's experiment
Taneda has made some of the most compelling photographs of flow past a cylinder, including this one featured on the cover of Van Dyke's book. In some respects the Cats2D simulation agrees well with this photograph. The cusps and curls are slightly more developed in the simulation than in the experiment. Some diffusion is also evident in the experiment. These differences are minor. There is a large difference in the width of the street, however.

I've annotated the photograph to define a length that I tried, without success, to match with a Cats2D simulation. I estimate L = 5.4D in this photograph. All my simulations at Re = 140 give a value in the range 4.5 to 4.7, about 15% less than the experiment. I tried many things to make L larger, such as varying the channel width, the inlet velocity profile, and the outlet boundary condition, without success.
I have also noticed that the eddy on the lower right in Taneda's photograph is badly out of line with its neighbors, and has an unusual smudged appearance. In other experiments, and in my simulations, eddies form two parallel lines a narrow distance apart. The uneven rows of eddies in the Taneda photograph suggests some sort of irregularity in the experiment.
Taneda's photograph was the first that I tried to reproduce with a simulation, and it bothered me that I could not match this length better. Later I found I could reproduce Tritton's experiments satisfactorily, and also Homann's on the reasonable premise that he systemically overestimated the Reynolds numbers in his experiments. Their experiments both exhibit a narrower vortex street, much closer to the simulations. Indeed, Homann's vortex street is slightly narrower than predicted by the simulations.
It was only near the end of writing this article that I compared Cats2D to figure 96 in Van Dyke, showing Taneda's photograph at Re = 105. This photograph matches the Cats2D simulation remarkably well in every aspect, including width of the street and lateral spacing of the two lines of eddies.

I have no doubt that Cats2D produces the correct solution to the incompressible Navier-Stokes equations for the boundary conditions and input data given. The physical properties and dimensions of the experiments are easily obtained to high accuracy, so it is primarily the boundary conditions that introduce disagreement between model and experiment. In a sense, the nearly perfect agreement between experiment and simulation shown here validates the care taken by the experimentalist to achieve an accurate physical representation of the idealized conditions of the model, that of a free stream flow unaffected by walls or inlet/outlet conditions.
Unsteady oscillations, 175 < Re < 300
In a well designed experiment, vortex shedding will occur parallel to the cylinder axis with constant frequency and amplitude up to Reynolds number around 150. In this regime, flow is nearly two-dimensional in the plane of the cylinder cross-section. Oblique shedding has been observed at Re < 100, but this effect is only weakly three-dimensional. Stronger three-dimensional effects are observed as Reynolds number nears 200. Flow becomes noticeably irregular in both frequency and amplitude. Two unstable modes have been identified, both of them three-dimensional. Williamson's Annual Review paper describes them in detail. Since I am only concerned with two-dimensional flows I won't say more about three-dimensional modes here.
There are also unstable modes in this regime that are purely two-dimensional. Since flow in the streamwise plane is not badly disturbed from a two-dimensional state in this regime, these modes might have some bearing on behavior. In the simulation on a wide domain, two-dimensional fluctuations are disordered at Re = 300, which is obvious in the animation below.

This visualization is inspired by a photograph found in Van Dyke's album (table of contents page) showing smoke streaklines in a wind tunnel.

The vortexes are swept back more in the experiment than in the simulation, but this is partly an issue of perspective, because the photograph was taken at an upward angle rather than perpendicular to the plane. Flow also appears to be less disordered in the experiment. Channel width in the simulation is one hundred times larger than cylinder diameter, so perhaps the wind tunnel experiment shown here was done in a narrower channel. Reducing channel width by a factor of five is strongly stabilizing. The simulation on the narrow domain remains regular up to Re = 260, and nearly so at Re = 300, which is animated below.

This simulation resembles the experiment more closely than the previous one, but the comparison should not be taken too seriously, because flow in the experiment is likely to have significant three-dimensional characteristics not captured in the two-dimensional model.
Impulsive startup
Whereas the previous sections considered fully developed flows, whether steady or oscillatory, these next comparisons focus on time-dependent behavior when a cylinder is first set into motion in a stationary bath. Reynolds numbers in these simulations are much higher, in the turbulent regime for fully developed flow, but flow is laminar at the short times shown here.
Impulsive start of a cylinder at Ut/D = 1.92 for Re = 1700 is shown in this photograph by Honji and Taneda (1969), from figure 61 in Van Dyke's An Album of Fluid Motion. I have enlarged the area where two small vortexes form upstream of the main vortex. Simulations by Cats2D agree very nicely with the photograph.
This next photograph, by M. Countanceau and R. Bouard, is from figure 59 in Van Dyke. The photograph views the cylinder surface at an oblique angle, which slightly distorts the comparison with the two-dimensional simulations, so I haven't fussed too much with the scale and alignment of the images. Re = 5000, Ut/D = 1.0.


Here is the same flow at a later time, Re = 5000, Ut/D = 3.0.


Agreement between experiment and simulation is excellent, but Cats2D reveals more precisely the arrangement of vortexes than can be deduced from the photograph.
6. Predicting the critical Reynolds number for onset of periodic flow
At Reynolds number somewhere around 40 to 50, steady flow becomes unstable. A wake forms behind the cylinder that is laminar with stable amplitude and period. A Hopf bifurcation is responsible for the transition. This seems have been first identified by Mathis, Provensal, and Boyer (1984) and described further in Provensal, Mathis, and Boyer (1987). Based on wind tunnel tests they extrapolate the critical Reynolds number to 47 for the unbounded case. Around this time Jackson reported a value of 46, based on numerical studies. Williamson puts it at 49 in his review article. Tritton's experiments show that it happens at a lower value, near 40. Taneda offers this same number. Homann's number, around 55, is an outlier. My results computed by Cats2D range from 39 to 48, with lower values observed on larger domains.
Eigenanalysis predicts a critical Reynolds number equal to 39.0 in the wide channel, and 46.0 in the narrower channel. Here are growth rates for the leading mode:
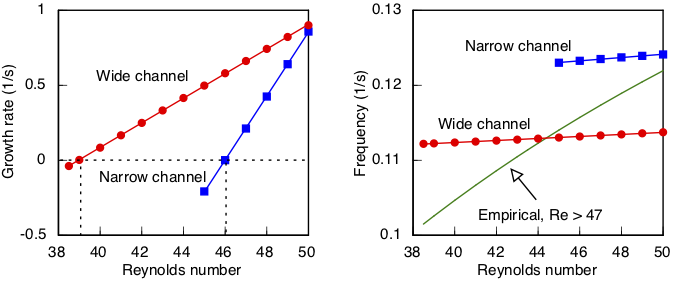
Time histories for streamfunction at the trailing point of the cylinder in the wide channel are shown below at progressively larger Reynolds numbers. This value represents the difference in flow rates over the top and bottom of the cylinder. Even very close to the bifurcation, the amplitude of the oscillation does not seem to diminish. Also, the oscillation is not perfectly symmetric about zero, which indicates that the wake is displaced slightly to the left or right of the channel centerline. Although the precise manifestation of this effect quantified here is possibly an artifact of discretization error in the simulation, it also reflects on the inherent sensitivity of the physical problem to small disturbances.
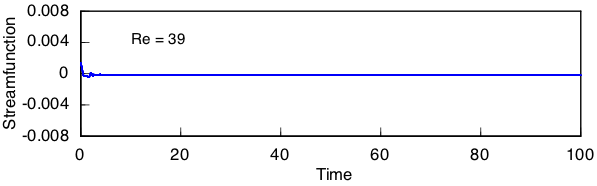
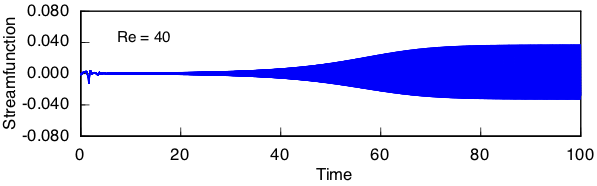
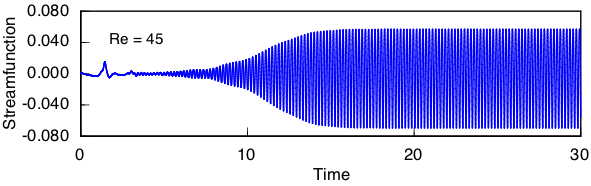
Streaklines at the same Reynolds numbers are shown below. The onset of large amplitude motion in the wake is quite sudden.



It takes only a small kick to send this flow cartwheeling into nonlinear instability.
The streamfunction time histories for Re <= 45 shown earlier show oscillations of uniform amplitude at a single frequency, suggesting that only one complex eigenmode has become unstable. A more complex behavior emerges at slightly higher values, illustrated by this result computed at Re = 47.5:
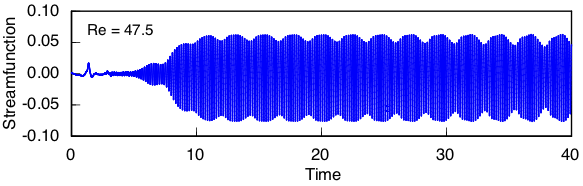
A secondary oscillation has emerged in which the amplitude varies at a frequency fifteen times slower than the base oscillation. Eigenanalysis reveals that a second complex eigenmode becomes unstable at Re = 43.4. Its period is 14/15 of the first mode, which explains the slow secondary beat.
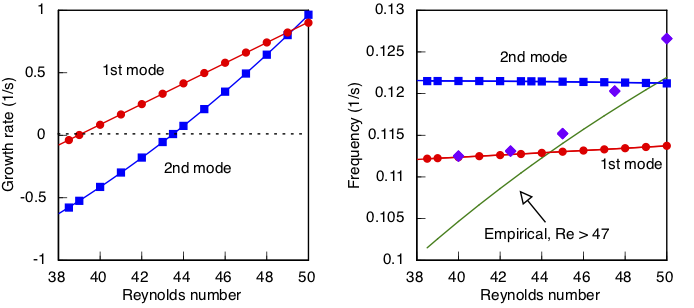
Note that the growth rate of the two modes is nearly equal at Re = 47.5, hence their strong interaction.
None of this happens in the narrow domain, where a single mode becomes unstable at Re = 46.0. Apparently reducing the width of the channel has a stabilizing effect in this regime, but the absence of a second unstable mode nearby bears further investigation. Where did it go?
In these next plots I show that reducing channel width from 50 diameters to 20 diameters on each side of the cylinder is strongly stabilizing for the first mode but only weakly so for the second mode. In the narrowest channel here, only the second mode is unstable at these Reynolds numbers.
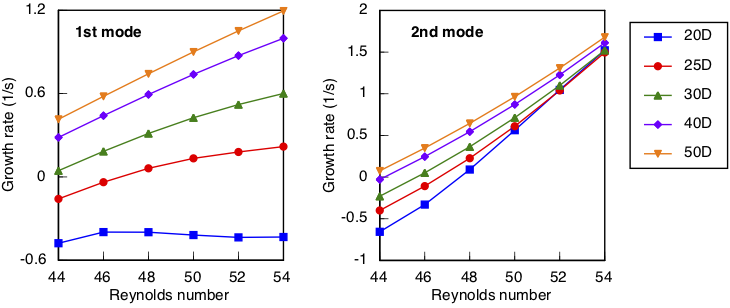
In this next streamfunction time history, I have started with a fully developed solution at Re = 140 in the narrow channel and reduced the Reynolds number to a value just below the critical value. Oscillations die out as expected from the eigenanalysis.
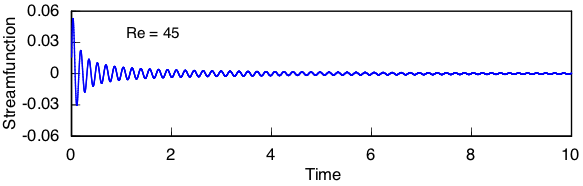
This procedure is repeated at a Reynolds number just above the critical value, and the oscillations persist at a lower amplitude.
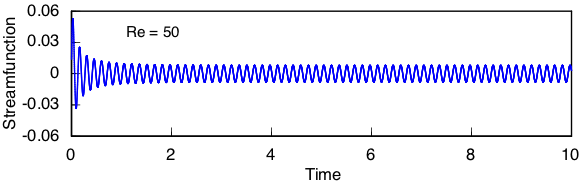
Since only one unstable mode is active in the narrow channel, we don't see any secondary beat in the oscillations.
Experimentalists have reported a wide range of Reynolds number for this transition, roughly between 40 and 55 for experiments in liquids, and much higher in wind tunnel experiments where the cylinder is close to the walls. My simulations show that the instability can be found at the lower end of this range if the domain is large enough. But I think the simulations also suggest that there is no one correct answer. It is difficult to realize the idealized behavior of a free stream in an infinite domain at long time in either the experiments or the simulations.
7. Transition to unstable period and amplitude, Re > 175–260
This transition is not quite so well defined as the discussed in the previous section. For Re < 140 there usually is only a single frequency to the oscillations. This state is considered stable in the sense that the period and amplitude are constant. But we have already seen a situation for 45 < Re < 50 in which two modes with different periods interact. Another situation in which two modes appear to interact is shown here at Re = 140, where secondary peaks are caused by a harmonic at twice the frequency of the dominant mode. Nevertheless, the frequency and amplitude of these modes is perfectly steady.
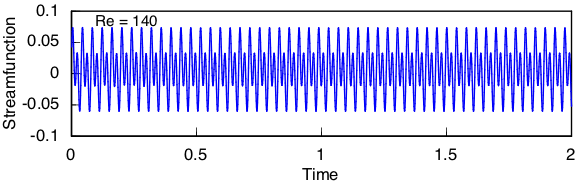
The transition we are looking for is characterized by a change from order to disorder in the vortex street, which happens when the the amplitude and period begin to vary over time to an obvious degree. Linear stability analysis cannot be applied under these conditions, so I have used time integration of the nonlinear equations to pinpoint the transition.
The earliest hint of a transition I see is found at Re = 170, where the amplitude has begun to vary slightly and the secondary peaks have diminished greatly in size.
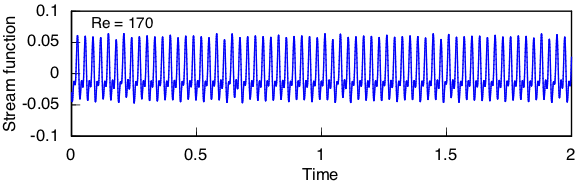
At Re = 175 the variation in amplitude has grown larger and the secondary peaks are nearly gone. The main peaks remain nearly regular in frequency, however.
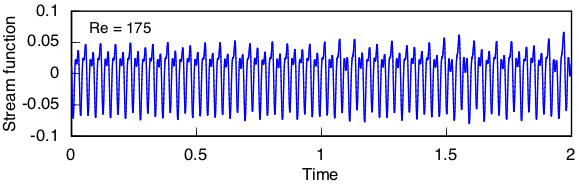
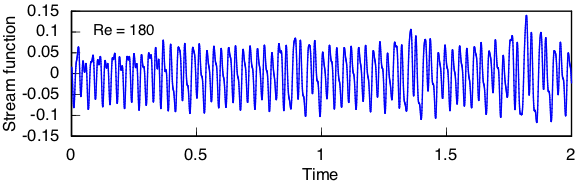
At Re = 180 the amplitude and frequency both vary significantly, and secondary peaks can no longer be discerned, but the situation appears only mildly disordered.
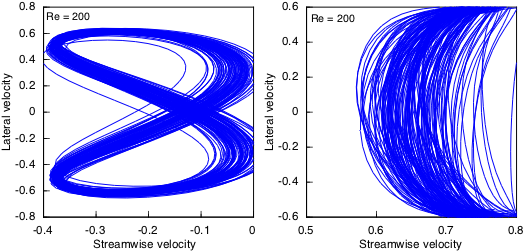
Another way to detect and display the breakdown of regular periodic behavior is to plot the U and V velocity components as an orbit over the course of many periods. In a regular periodic flow, the orbits will retrace the same line over and over. As periodic behavior grows more complex, orbits begin to wander, and when it breaks down, orbits become chaotic. This shows up quite visibly. Orbits are plotted below for two points on the center axis of the channel. At a point immediately behind the cylinder (X=1,Y=0), the limit cycle begins to degrade for Re > 175.
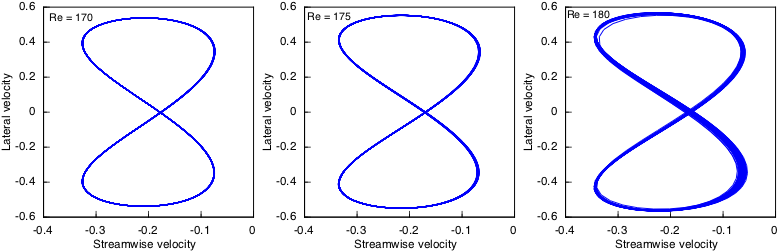
The degradation is more obvious downstream (X=10,Y=0).
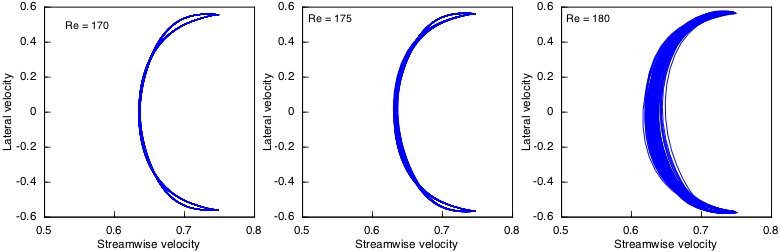
Undoubtedly order is breaking down by Re = 180, but there still remains some semblance of a dominant period.
At Re = 200 the amplitude and frequency are quite irregular. There no longer appears to be any dominant period.
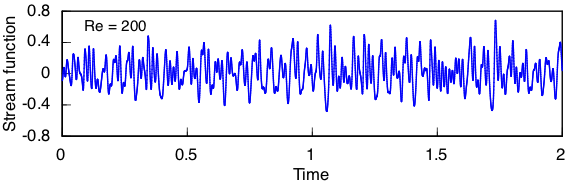
Flow remains laminar, but these orbits suggest it is nearing the threshold for turbulence.
These results were computed on the wide domain. As noted earlier, the solution on the narrow domain remains periodically stable up to Re = 260. But the simulations can only predict two-dimensional behavior. Three-dimensional modes are present at much lower values, around Re = 190 or less, so caution should be exercised intepreting the two-dimensional simulations in this regime.
8. The nature of vortex shedding
At the start of this article I summarized five transitions identified in chapter 3 of Tritton's book. I have analyzed three of them so far. These are steady flow separation, oscillatory wake flow, and unsteady vortex shedding. The final transition, to turbulence, is beyond the scope of this work.
There is one transition I have not discussed yet: Tritton asserts that vortexes remain attached to the cylinder up to Reynolds number around 100, beyond which vortex shedding is first observed. Notably Williamson does not identify any such transition in his review article. My simulations show that it does not exist as a separate transition. Vortexes are shed when an oscillating wake first forms. Vortex shedding at Re = 50, shown below, looks essentially the same as it does at Re = 140, shown in section 3 above.
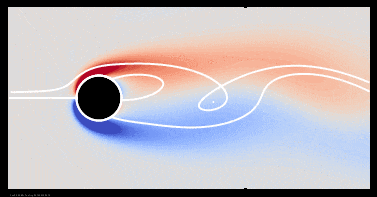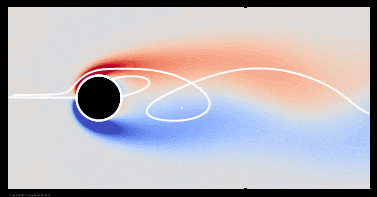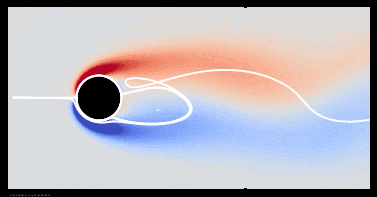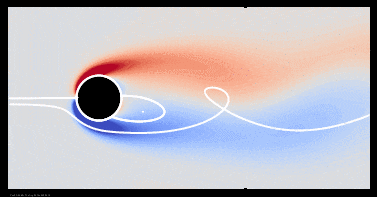
There is nothing to distinguish the generic behavior of the vortex street for Re > 100 from its behavior at lower Reynolds numbers, except that we can detect an eddying motion against the background motion easily with our eye. At lower Reynolds numbers the rotation is still there, but is too slow to easily perceive by common techniques of experimental visualization.
There are a couple of issues to sort through here. One is how we perceive a vortex. Colloquially, a vortex or eddy is a region of whirling or swirling flow, in which fluid moves in a circular or spiral path. Sometimes an eddy is described as a movement counter to the main current. Particles appear to flow upstream because they move downstream more slowly than nearby particles. This is one of those "I know it when I see it" definitions that is not precise enough to draw useful conclusions in a formal analysis of a complex time-dependent flow. If our eye can travel far enough and fast enough downstream to offset the main current, we might be able to perceive a swirling motion superimposed upon it. But maybe not.
The other issue is how we define a vortex. In a two-dimensional incompressible flow, a vortex is a region in which streamlines form closed curves, within which fluid recirculates indefinitely. It can be readily defined by its separation and stagnation points and the streamlines that intersect them. The wake behind a cylinder is described by Tritton and others as vortexes that have detached from the cylinder and flowed downstream. However, the instantaneous streamlines and particle paths are wavy downstream of the cylinder, but do not intersect themselves to form vortexes by this definition.
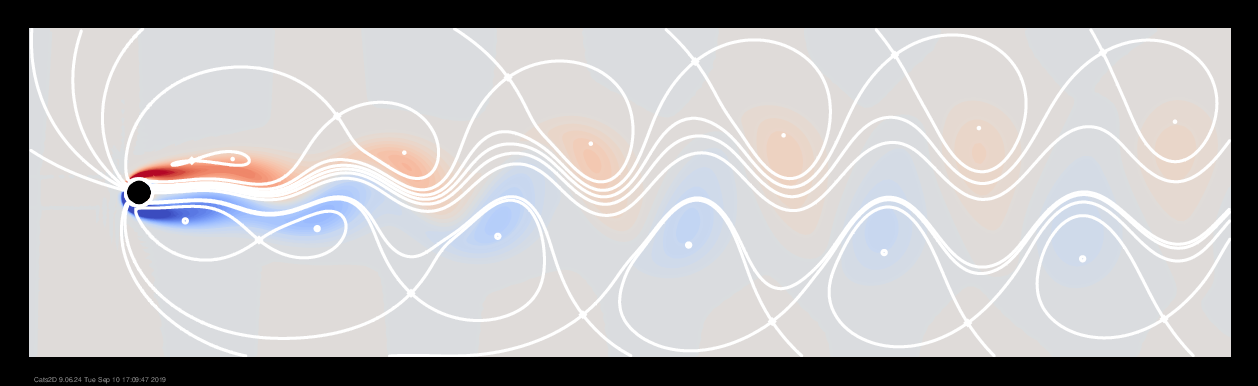
To bring the colloquial and formal definitions of a vortex into agreement, we need to adopt a reference frame that moves with the main current of the flow. The meaning of main current itself is subject to definition, but in flow past a cylinder, the main current is simply the free stream flow. Recasting the flow in this reference frame and plotting its streamlines reveals a well defined line of vortex centers at Re = 50:

To better understand how these vortexes are arranged it helps to plot the saddle and separation streamlines:
Vortexes are more intense and more closely spaced at Re = 140, which makes them easier to visually detect against a moving current:
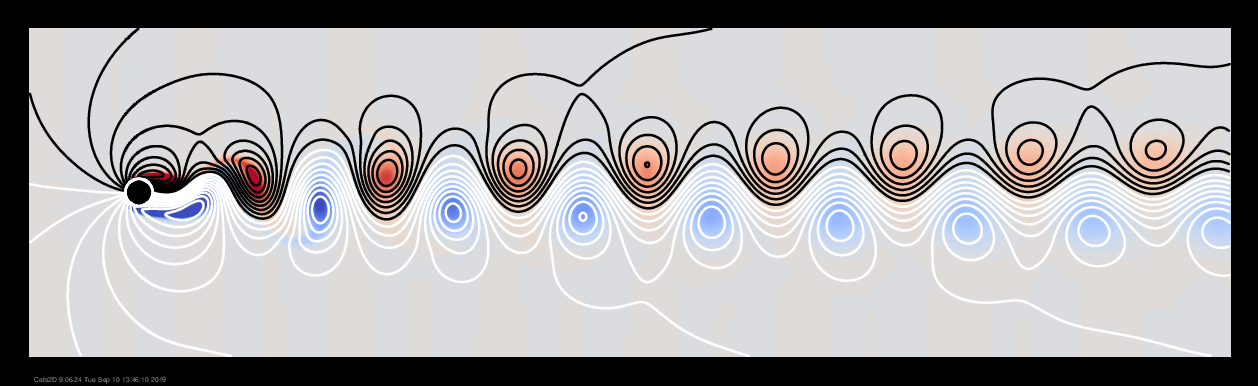
However, saddle and separation streamlines show that flow is unchanged qualitatively:
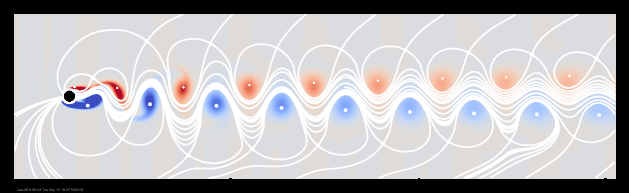
In this view, vortexes are spun off from a cylinder and left behind as it moves through a stagnant liquid, as shown by this streakline animation in the moving reference frame:

Viewing the flow in a reference frame that moves with the free stream not only allows us to see the vortexes, it allows us to precisely define them in terms of centers and saddles, without needing to rely on vorticity as a proxy. We can plot the positions of the vortex centers at various times to determine the paths they follow downstream. They travel in two lines that gradually increase in spacing downstream, as shown here for Re = 90:
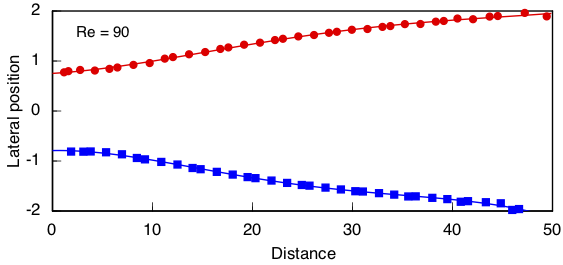
The spacing between the vortexes along each line reaches a maximum a short distance behind the cylinder, and slowly declines until near the outflow boundary, which has obviously perturbed the vortex street. This shows the importance of locating this boundary far away from the cylinder.
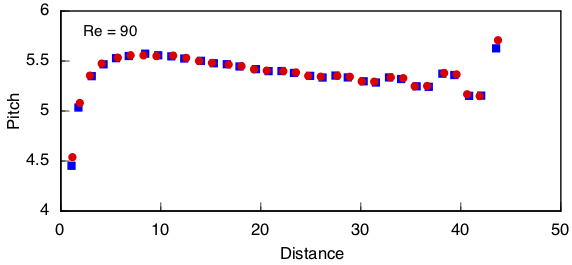
The lines traced out by vortex centers in a moving reference frame tend to a spacing of 1.54 at the cylinder where the vortexes are born (first figure). The pitch between adjacent vortex centers rises from zero to a maximum value of 5.57 within 8 cylinder diameters downstream, then declines slowly (second figure). The spacing ratio, 1.54/5.57 = 0.277, is close to 0.281, the value extracted by Von Kármán using linear stability analysis on an infinite array of point vortexes.
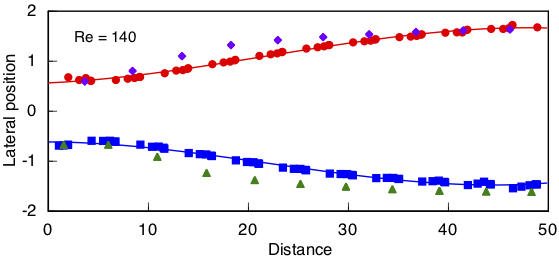
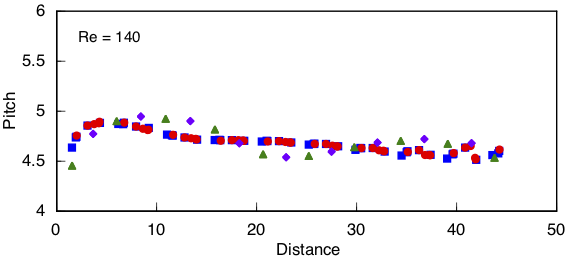
Repeating this step at Re = 140 gives a spacing ratio of 1.30/4.89 = 0.266, using simulations from the wide domain (red circles and blue squares). I've also included symbols for the narrow domain (purple diamonds and green triangles). The closeness of the channel sides in the narrow domain noticeably affects the lateral span of the vortex street. Nevertheless, the vortex street tends to the same width at the cylinder as found in the wide domain.
The pitch is relatively flat over much of the channel in the wide domain. It oscillates somewhat in the narrow domain, though not very much.
The simulations demonstrate that vortex shedding does not undergo any significant qualitative change between onset of wake formation at Re = 40 and the transition to unsteady oscillation at Re = 175.
9. Wrap up
I am finding that it takes every tool in the kit to understand a time-dependent flow. Streamlines, particle paths, or streaklines are not enough on their own. It really takes all three of them. Quantitative measures are needed, too. Critical point plots and eigenanalysis contribute more insights. I think every tool invoked in this study added value to it. I say this because I don't believe there is any commercial software available today that could be used to replicate this analysis to any great extent without extraordinary effort.
Appendix — Unstable steady state solutions, Re > 40
For Reynolds number greater than approximately 40, an unstable wake forms, yet steady state solutions can be computed to much higher values of Re. A turning point is encountered at Re = 405. Streamlines are shown here on the stable side of the turning point.
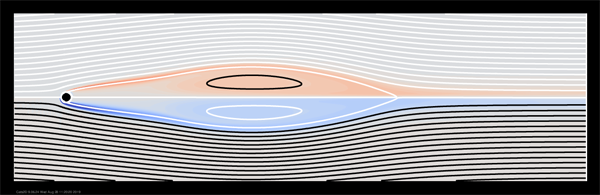
The vortexes attached to the rear of the cylinder have grown enormously large. This solution is only stable in the sense that no real eigenmodes have crossed the imaginary axis. It will never be realized in practice because the solution is highly unstable to the Hopf bifurcation that causes the wake to oscillate at much lower Reynolds number.
Proceeding around the first turning point, we head towards lower Reynolds number and find another turning point at Re = 242. A second real eigenvalue crosses the axis at this turning point, making the steady solution doubly unstable to real modes. This branch can be followed to much higher Reynolds number, but it is uninteresting. Below I show streamlines at Re = 300 on the three branches thus identified:
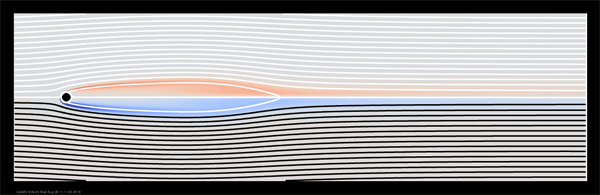
—Zero unstable real modes (first branch, 0 < Re < 405)
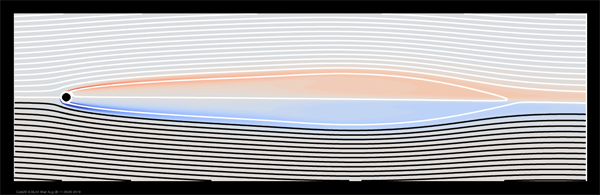
—One unstable real mode (second branch, 405 > Re > 242):
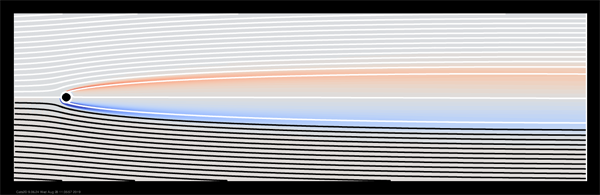
—Two unstable real modes (third branch, 242 < Re < ?)
Everyone knows this flow develops an oscillatory wake at low Reynolds numbers, so the existence of these steady solutions is unlikely to fool anyone. However, very few types of flow are understood nearly so well as this one. Approaching this flow blindly, it is easy to compute these solutions, but difficult to detect their instability to the Hopf bifurcation. Perturbing the flow and integrating for a long time is necessary. Detecting the Hopf bifurcation by computing eigenvalues is really hard unless you already know its period. It is easy to go astray when simulating a flow that is less familiar.
There is another small point of interest in all this. At the second turning point, a second real mode crosses the imaginary axis, therefore both branches connected to this turning point are unstable. Many people know that a turning point marks a change of stability, but a commonly held misunderstanding is that an unstable flow will always return to stable at a turning point. This happens when a real mode that crosses the imaginary axis at the first turning point returns to the left hand side of the complex plane at the second turning point. But it also sometimes happens as shown here that an additional mode goes unstable, making an unstable solution more so.
